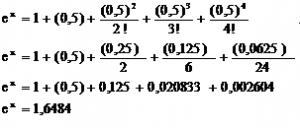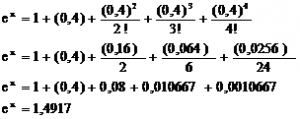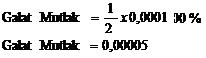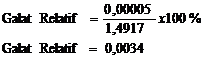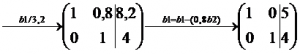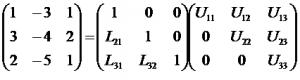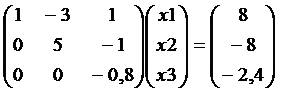1501167380 – Angela Muliawan

SOAL  TUGAS   GSLC 1- METODE NUMERIK

Angela Muliawan

1501167380/06PFT

1.     Perusahaan tambang yang sedang melakukan eksplorasi melakukan penelitian kandungan emas disuatu tempat. Berdasarkan hasil penelitian, kandungan emas mengikuti jalur lintasan y=f(x) = e^x  . Menurut data satelit, untuk mendapatkan kandungan emas terbanyak ada di posisi x=0.4. Jika posisi pengeboran tersebut dihitung menggunakan pendekatan deret Taylor sampai dengan 4 suku pertama, hitunglah ( pembulatan 4 angka dibelakang koma),Hitunglah :

a. Nilai f(0.5) untuk fungsi f(x) = e^x

b. Galat mutlak dan relatifnya.  Nilai  e   = 2,7183

Jawab :

1. F ( 0,5) = e^x

Jadi, f(0,5)  =1,6484

2. Galat mutlak dan relatifnya

SPT = 0,00001 (Untuk 4 angka dibelakang koma)

Maka, Galat Mutlaknya adalah 0,00005 dan Galat Relatifnya adalah 0,0034

2.   Seorang pembuat boneka ingin membuat dua macam boneka yaitu boneka A dan boneka B. Kedua boneka tersebut dibuat dengan menggunakan dua macam bahan yaitu potongan kain dan kancing. Boneka A membutuhkan 10 potongan kain dan 6 kancing, sedangkan boneka B membutuhkan 8 potongan kain dan 8 kancing. Permasalahannya adalah berapa buah boneka A dan boneka B yang dapat dibuat dari 82 potongan kain dan 62 kancing ? Selesaikan dengan metode gauss-Jourdan !

Jawab :

Jadi, yang dapat dibuat dari kain dan kancing tersebut adalah 5 buah boneka A dan 4 buah boneka B.

3. Carilah nilai  x₁, x₂ dan x₃  dari sistem persamaan linear berikut dengan menggunakan metode  dekomposisi LU.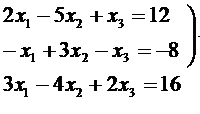

Jawab :

Dari persamaan diatas maka didapat :

–          U₁₁ = 1

–          U₁₂ = -3

–          U₁₃ = 1

–          L₂₁. U₁₁ = 3

L₂₁ = 3

–          L₂₁. U₁₂ + U₂₂ = -4

U₂₂ = 5

–          L₂₁.U₁₃ + U₂₃ = 2

U₂₃ = -1

–          L₃₁.U₁₁ = 2

L₃₁ = 2

–          L₃₁.U₁₂ + L₃₂.U₃₂ = -5

2.(-3) + L₃₂.5 = -5

L₃₂ = 0,2

–          1 = L₃₁.U₁₃ + L₃₂.U₂₃ + U₃₃

1 = (2.1) + (-0,2) + U₃₃

U₃₃ = -0,8

Hitung Untuk L.y = b

–          y₁ = 8

–          3y₁ + y₂ = 16

y₂ = -8

–          2y₁ + 0,2y₂ + y₃ = 12

16 – 1,6 + y₃ = 12

y₃ = -2,4

Hitung U.x = y

–          (-0,8)x₃ = -2,4

x₃ = 3

–          5x₂ – x₃ = -8

5x₂ -3 = -8

x₂ = -1

–          x₁ – 3x₂ + x₃ = 8

x₁ + 3 + 3 = 8

x₁ = 2

Maka nilai dari x₁, x₂ dan x₃ nya adalah 2, -1, 3

www.binus.ac.id